As a first example of useful combinational logic, let's build a device that can add two binary digits together. We can quickly calculate what the answers should be:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 102
So we well need two inputs (a and b) and two outputs. The low order output will be called Σ because it represents the sum, and the high order output will be called Cout because it represents the carry out.
The truth table is
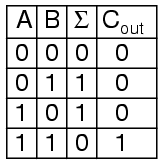
Simplifying boolean equations or making some Karnaugh map will produce the same circuit shown below, but start by looking at the results. The Σ column is our familiar XOR gate, while the Cout column is the AND gate. This device is called a half-adder for reasons that will make sense in the next section.
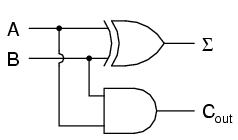
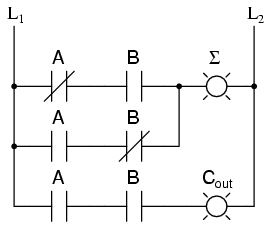
or in ladder logic
[http://www.malayalam.net/howto/LessonsInElectricCircuits/Digital/DIGI_9.html]





